一般线性模型的几种常见形式及其合理选用

www.cnkang.com 2007-1-13 10:42:00 中华康网

　　【提　要】　目的　展示一般线性模型(GLM)的常见形式及其特点，便于人们合理选用。方法　通过改变设计矩阵X和误差的协方差矩阵Ω的结构以及分析设计矩阵X的变量性质，将GLM演绎成一个个简单明了的具体表达式。结果　将GLM简化成适用于回归分析、方差和协方差分析、多水平模型等具体的统计模型。结论　合理选用统计模型的关键在于弄清资料所取自的设计类型，影响因素和反应变量的性质，有无协变量以及各种统计模型的适用范围。

Common Patterns and Rational Applications of the General Linear Model

Hu Liangping,

　　Department of Medical Statistics,Academy of Military Medical Sciences(100850),Beijng

　　【Abstract】　Objective　Presenting the common patterns and their characteristics of the general linear model(GLM)for the convenient and rational application.Methods　By changing the structures of design matrix(X)and covariance matrix of error(Ω) and analyzing the characters of variables in the design matrix(X),some concise and concrete expressions are deduced from GLM respectively.Results　To simplify GLM into several particular statistical models which are suitable for regression analysis,analysis of variance and covariance,and multilevel modelling.Conclusion　The key to the rational selection of statistical models lies in clarifying the design types of data,the characters of affecting factors and response variables,the availability of covariates,and the applicability of various statistical models.

　　【Key words】　General linear model　Design matrix　Covariate matrix　Multilevel model

　　一般线性模型概述

　　统计分析的对象是统计资料，如果资料中包含着自变量X和连续变化的反应变量Y时，为了用最简便的方式描述反应变量与自变量之间的依存关系，人们首选一般线性模型(GLM)，见式(1)。

Y=Xβ+e

(1)

　　模型(1)中，Y为反应变量的观测值向量，X为由自变量构造的设计矩阵，β为回归参数向量，e为正态独立随机误差向量，并假定其均值E(e)=0，协方差矩阵为Ω=Cov(e)。

　　当由模型(1)定义的GLM具有各种不同结构的设计矩阵X和误差的协方差矩阵Ω时，GLM就会有各种不同的变形。例如：当Ω=σ2In时，模型(1)被称为经典(或标准)线性回归模型；如果可将X剖分成X=(X1,X2)，其中X1与固定效应有关，X2与随机效应有关，同时，Ω具有式(2)的形式：

Ω=X2VX′2+Ψ

(2)

　　式(2)中V和Ψ是协方差矩阵，则模型(1)就变成一般线性混合模型(GLMM)；如果对X与Ω作其他一些假定，模型(1)可分别转变成MANOVA模型(即多元方差分析模型)和GMANOVA模型(即广义多元方差分析模型)等模型〔1〕。

　　从构成设计矩阵X的变量性质来分类，模型(1)又有许多不同的变形。例如：当X分别由固定效应、随机效应和固定与随机两种效应的定性影响因素构造而成时，模型(1)就分别简化为固定效应、随机效应和混合效应的方差分析模型；当X全部由定量的影响因素(包括哑变量)构造而成时，模型(1)就简化为回归分析模型；当X同时由定性和定量两种影响因素构造而成时，需分以下三种情形来讨论：情形一，当定性的影响因素是固定效应时，模型(1)就变成了协方差分析模型；情形二，当定性的影响因素是随机效应时，模型(1)就变成了多水平回归模型(亦称随机系数模型或分层模型)〔1～3〕；情形三，当定性的影响因素包括固定和随机两种效应时，若固定效应的定性变量未用哑变量技术处理，模型(1)就变成了具有协方差分析结构的多水平模型；反之，模型(1)仍旧是多水平回归模型。

　　GLM常见的简化形式

　　1.方差分析模型

　　(1)固定效应方差分析模型及F统计量

　　由于多因素实验设计类型很多，今以两因素析因设计为例(下同)。设固定效应因素A、B分别有a、b个水平，共有a×b种水平组合，各组合下均重复k(k≥2)次实验，Y为定量的反应变量，则与这个两因素析因设计对应的方差分析模型由式(3)给出：

yijk=μ+τi+βj+(τβ )ij+eijk

(3)

i=1,2…,a;j=1,2,…,b;k=1,2,…,n。

　　模型(3)中，μ是总平均效应，τi是因素A第i个水平的效应(即τi=μAi-μ)，βj是因素B第j个水平的效应(即βj=μBj-μ，(τβ　)ij是A与B分别在第i水平与第j水平组合条件下的交互作用的效应，eijk是随机误差分量，且

　　进行方差分析时，需要构造出F统计量，其方法是推导出因素A、B及交互作用A×B的期望均方，详见文献［4］。依据三个期望均方的表达式，构造出检验“H0:τi=0,H0:βj=0,H0:(τβ　)ij=0对一切i,j”的三个F统计量，见式(4)。

FA=MSA/MSE、FB=MSB/MSE、FAB=MSAB/MSE

(4)

　　式(4)中，FA～Fa-1，ab(n-1)分布，FB～Fb-1,ab(n-1)分布，FAB～F(a-1)(b-1),ab(n-1)分布。

　　(2)随机效应方差分析模型及F统计量

　　如果某因素的水平是从较大的总体中随机选取的，那么，关于该因素的推断将会对所研究的总体的全部水平都有效，称这种因素为随机效应因素。现仍以两因素析因设计为例，来研究随机效应方差分析模型。在上述关于模型(3)的“假设条件”中，将固定效应因素A、B改为随机效应因素，其他条件不变，此时，处理资料的模型见式(5)。

yijk=μ+τi+βj+(τβ )ij+eijk

(5)

i=1,2,…，a;j=1,2,…,b;k=1,2，…，n。

　　模型(5)中，μ是总平均效应，τi,βj,(τβ )ij以及eijk都是随机变量。特别地，假定τi～NID(0，στ2)，βj～NID(0，σβ2)、(τβ )ij～NID(0，στβ2)、eijk～NID（0，σ2)。

　　于是，任一观察值的方差是：

V(yijk)=στ2+σβ2＋στβ2＋σ2

(6)

　　式(6)中等号右边四项叫做方差分量，故模型(5)又称为方差分量模型。

　　对于方差分量模型，构造F统计量的方法仍是推导出A、B及A×B的期望均方，详见文献［4］。依据三个期望均方的表达式，构造出检验“H0∶στ2=0;H0∶σβ2=0;H0∶στβ2=0”的三个F统计量(因为对随机效应因素来说，检验关于各个处理效应的假设是没有意义的)，见式(7)。

FA=MSA/MSAB

　　FB=MSB/MSAB

　　FAB=MSAB/MSE

(7)

　　式(7)中，FA～Fa-1,(a-1)(b-1)分布，FB～Fb-1,(a-1)(b-1)分布，FAB～F(a-1)(b-1),ab(n-1)分布。

　　(3)混合效应方差分析模型及F统计量

　　当因素A为固定效应、因素B为随机效应因素时，分析这种两因素析因设计资料的模型称为混合效应方差分析模型，见式(8)

yijk=μ+τi+βj+(τβ )ij+eijk

(8)

i=1,2,…,a;j=1,2,…,b;k=1,2…,n。

　　模型(8)中，τi是固定效应，βj是随机效应，并且假定(τβ )ij也是随机效应，而eijk是随机误差。还假定τi使得Σai=1τi=0、βj～NID(0,σβ2)、(τβ)ij～N(0，σ2τβ)、eijk～NID(0,σ2)。(τβ )ij的独立性并不总能成立，因为Σai=1(τβ )ij=(τβ).j=0,j=1,2,…，b。这意味着，固定因素的不同水平上的某些交互作用元素不是独立的。且

　　基于模型(8)的方差分析，仍需借助期望均方来导出F统计量，关于A、B、A×B期望均方表达式，详见文献［4］。对于固定效应的检验假设为H0∶τi=0，对于随机效应的检验假设为H0∶σβ2=0;H0∶στβ2=0。此时，恰当的F统计量如式(9)所示。

FA=MSA/MSAB

　　FB=MSB/MSE

　　FAB=MSAB/MSE

(9)

　　式(9)中，FA～Fa-1,(a-1)(b-1)分布，FB～Fb-1,ab(n-1)分布，FAB～F(a-1)(b-1),ab(n-1)分布。

　　2.回归分析模型

　　当模型(1)中设计矩阵X全由定量的影响因素(允许有哑变量)构造而成时，它就简化成单纯的回归分析模型(10)。

yi=β0+β1X1+β2X2+…βmXm+ei

(10)

i=1,2,…,n。

　　模型(10)的参数估计、假设检验等内容在普通统计学教科书中都写得很详细，此处不再赘述。

　　3.单因素协方差分析模型与二水平模型

　　(1)单因素协方差分析模型〔4〕

　　在评价饲料营养价值的试验中，如果饲料的种类(设为因素A)是有限的a种，每个受试对象的平均进食量(X)对其平均体重增加量(Y)必有影响。这里A是固定效应的影响因素，X是定量的影响因素，Y是定量的观测结果，当全部受试对象被完全随机地分配进入a种饲料组中去接受试验后，所收集到的资料可用下面的含一个协变量的单因素协方差分析模型(11)来处理。

yij=μ+τi+β(xij-x..)+eij

(11)

i=1,2,…，a;j=1,2,…,n。

　　模型(11)中yij是第i种饲料组取得的反应变量的第j个观察值，xij是对应于yij的平均进食量，x..是全部xij的样本均值，μ是与yij对应的总平均值，τi是第i种饲料的效应，β是回归系数，eij～NID(0,σ2)是随机误差分量。于是，检验H0∶τi=0的F统计量见式(12)。

FA=［(SS′E-SSE)/(a-1)］/｛SSE/〔a(n-1)-1〕｝

(12)

　　式(12)中，FA～Fa-1,a(n-1)-1分布，SS′E=1yy-(1xy)2/1xx,SSE=Eyy-(Exy)2/Exx，此外，1xx，1yy，1xy分别为x,y,x与y的总离均差平方和及离均差积之和；Exx,Eyy,Exy分别为x,y,x与y的组内离均差平方和及离均差积之和。

　　(2)二水平模型〔2～3〕

　　在前述评价饲料营养价值的试验中，如果可供选用的饲料有成百上千种，今从此总体中随机地选取a种来做前述的试验研究，其他情况不变。此时，研究的目的是由a种饲料的试验信息去推测上千种饲料所构成的总体中y随x变化的依存关系。如果忽略饲料间变异对结果的影响，模型(1)一下简化成简单直线回归模型，但当模型在饲料间的变异是不可忽略的情况下，用简单的直线回归模型来描述是很不妥当的。此时，引入一个被称为二水平的(或随机系数)模型(13)是很合适的。

yij=ai+bixij+eij

(13)

i=1,2,…,a;j=1,2,…,n。

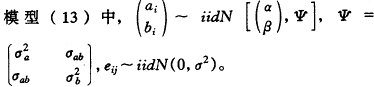
　　此处，截距ai、斜率bi都是随机系数，α、β分别为总体截距和斜率，Ψ为随机系数ai、bi的协方差矩阵，eij是正态独立随机误差。若令ai=α+a′i、bi=β+b′i，其中，a′i、b′i分别为截距和斜率的随机部分，则模型(13)变成模型(14)

yij=α+a′i+(β+b′i)xij+eij

　　=α+βxij+(a′i+b′ixij)+eij

(14)

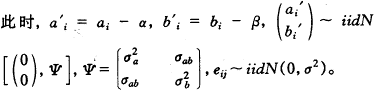
　　eij称为受试对象个体间(或称一水平上)的误差，而a′i+b′ixij则反映了饲料之间(或称二水平上)的误差，故称模型(14)为二水平模型。

　　(3)其他更复杂的协方差分析模型与多水平模型〔3，5〕

　　在所有固定效应的方差分析模型中，加入多个协变量，其对应的统计模型就称为相应设计的多元协方差分析模型；若固定效应全变成了随机效应(若仍残留某些固定效应，并用哑变量技术予以处理)，并且，这些随机效应因素有嵌套关系(如：学校＞班级＞教师＞学生)时，其对应的统计模型就称为多水平模型，若仍有部分固定效应因素未用哑变量技术处理，此时的模型就是具有多元协方差分析结构的多水平模型。

　　GLM各种变形的合理选用〔3,4〕

　　【例1】研究影响某种药丸重量的因素。随机选取4台生产此种药丸的机器和3位操作技师，并用配制出的同一批制药丸的半成品原料进行如下的试验。每位技师用每台机器重复2次试验，观测每片药丸的重量(定量观测值)，具体资料从略，假定资料满足正态性和方差齐性(下同)，试选择合适的统计模型处理资料。

　　【例2】为探讨某化学反应中温度和催化剂对收率的影响，研究者依据预试验的结果，选定了4种温度(70、80、90、100℃)和3种催化剂(甲、乙、丙)，对两因素所有可能的组合在相同条件下都重复2次试验，观测每次试验的收率(定量观测值)，具体资料从略，试选择合适的统计模型处理资料。

　　【分析与解答】从形式上看，例1与例2是相同的。但仔细琢磨，不难发现，它们之间是有区别的。在例1中，无论用哪一台机器制药，也无论是哪一位技师来操作，人们期望每片药丸的重量尽可能相等。但事实上，各药丸的重量不可能绝对相等，因为机器之间和技师之间都存在个体差异。由于每台机器和每位技师都是随机选取的，且对药丸重量影响的期望值是相同的，故机器和技师都可视为随机效应因素，适合选用两因素析因设计随机效应方差分析模型(5)处理资料。

　　而在例2中，不同温度和不同催化剂条件下的产率可能会相差很大，开展此项试验的目的就是要找到两因素最佳的水平搭配，故人们没有理由期望每次所得的产率应相等。也就是说，不能由试验中所涉及的4种温度的效应去推测各种温度的效应，同理，对催化剂也是如此。在本例中，将温度和催化剂视为固定效应更为合理，故适合选用两因素析因设计固定效应方差分析模型(3)处理资料。

　　【例3】设某市共有10个区县，某人试图研究该市10个区县哮喘患儿血清IgE平均水平之间的差别有无显著性意义时，考虑到患病病程长短可能是一个重要的定量影响因素。假定资料中仅包含区县、病程和IgE3个变量，具体资料从略，试选择合适的统计模型处理资料。

　　【例4】某研究者从一项关于儿童哮喘的全国性调查资料中随机地抽取了10个区县的资料，希望研究患儿血清IgE的水平高低与患病病程之间的依存关系，假定资料中包含的变量与例3相同，具体资料从略，试选择合适的统计模型处理资料。

　　【分析与解答】粗略地看完例3和例4后，给人的印象是它们说的完全是一回事。其实不然，在例3中，10个区县的调查资料全部用了，故区县是一个固定效应因素，研究目的是看各区县哮喘患儿血清IgE平均水平之间的差别有无显著性意义，但同时还必须消除病程的影响，故宜选用单因素10水平设计资料的协方差分析模型(11)。

　　而在例4中，欲分析的资料来自全国几百个区县随机抽取的10个区县的哮喘患儿，各患儿的血清IgE值不仅与患儿的病程有关，也在一定程度上受其所在区县的影响。也就是说，个体之间的差别是一水平上的误差，而区县之间的差别是二水平上的误差，分析的目的是希望由这10个区县资料去推测全国所有区县的情况，故分析此资料适合选用二水平模型(14)。因篇幅所限，其他统计模型的应用实例从略。

　　讨　论

　　GLM是统计模型中使用频率最高的，因为它有多种不同的变形，可分别适用于t检验、各种设计类型资料的方差和协方差分析、回归分析和多水平模型。面对各种实际资料，究竟应选择什么统计模型来处理合适，常是一个十分棘手的问题。正因为如此，在医学科研和医学期刊中，人们常误用统计分析方法，降低了科研工作的科学性〔7～9〕。

　　事实上，由于统计学内容十分丰富，除了可选用GLM和 GLMM外，有时还须选用广义线性模型、广义线性混合模型以及相应的非线性模型等。对于错综复杂的统计资料和千变万化的统计模型，即使是统计工作者，要做到时时都能合理运用统计学，恐怕也非易事。笔者认为：合理选用统计模型的关键在于弄清资料所取自的设计类型，影响因素的性质(固定或随机效应)，有无协变量、反应变量的性质(计量、计数、定性)和分布情况以及各种统计模型的适用范围。文中所述内容及肤浅看法，难免挂一漏万，甚至有欠妥之处，只是想借此文引起广大同仁们对我国科学研究各个领域内统计学应用方面普遍存在的问题的足够重视和关注，以期达到抛砖引玉之目的。

　　参考文献

　　1.Timm NH， Mieczkowski TA. Univariate ＆ Multivariate General Linear Models：Theory and Applicatious Using SAS Software。 North Carolina： SAS Institute Inc.1997，1—4，419—485.

　　2.Goldstein H. Multilevel statistical Models. Second Edition， London：Edward Arnold.1995，1—40.

　　3.Littell RC， Milliken GA， Stroup WW， Wolfinger. RD：SAS System for Mixed Models.North Carolina： SAS Institute Inc.1996，87—227，253—265，423—502.

　　4.Montgomery DC. Design and Analysis of Experiments.汪仁宫，陈荣昭译.实验设计与分析.北京：中国统计出版社，1998，222～252.

　　5.Singer JD. Fitting Multilevel Models Using SAS PROC MIXED. Multilevel Modelling Newsletter，1998，10(2)：5～8.

　　6.胡良平主编.现代统计学与SAS应用.北京：军事医学科学出版社，1996，129～145.

　　7.胡良平.医学科研与新药评价等工作中一个不可忽视的问题——轻视和误用统计学.军事医学科学院院刊，1996，20(3)：202～205.

　　8.胡良平，刘惠刚.医学期刊中常见统计错误分析.中华医学写作杂志，1998，5(2)：28～30.

　　9.胡良平.医学统计应用错误的诊断与释疑.北京：军事医学科学出版社，1999，1～105.